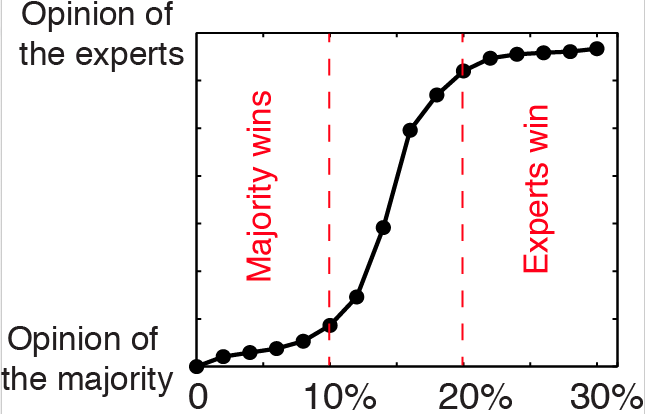
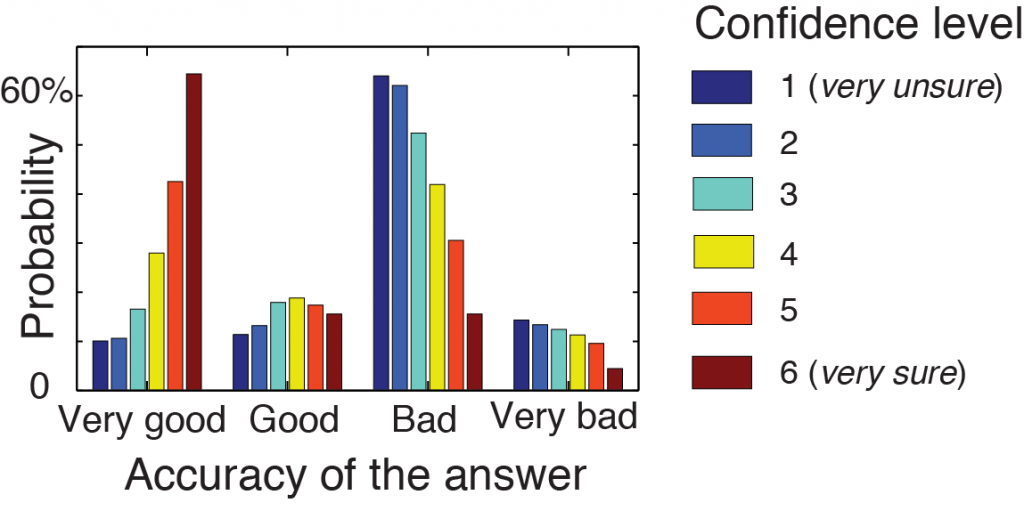
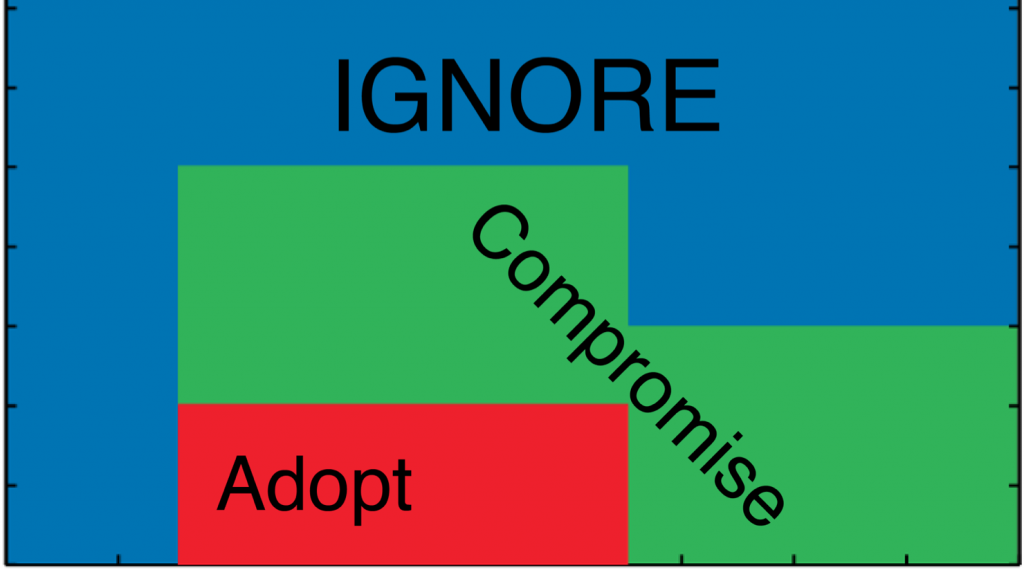
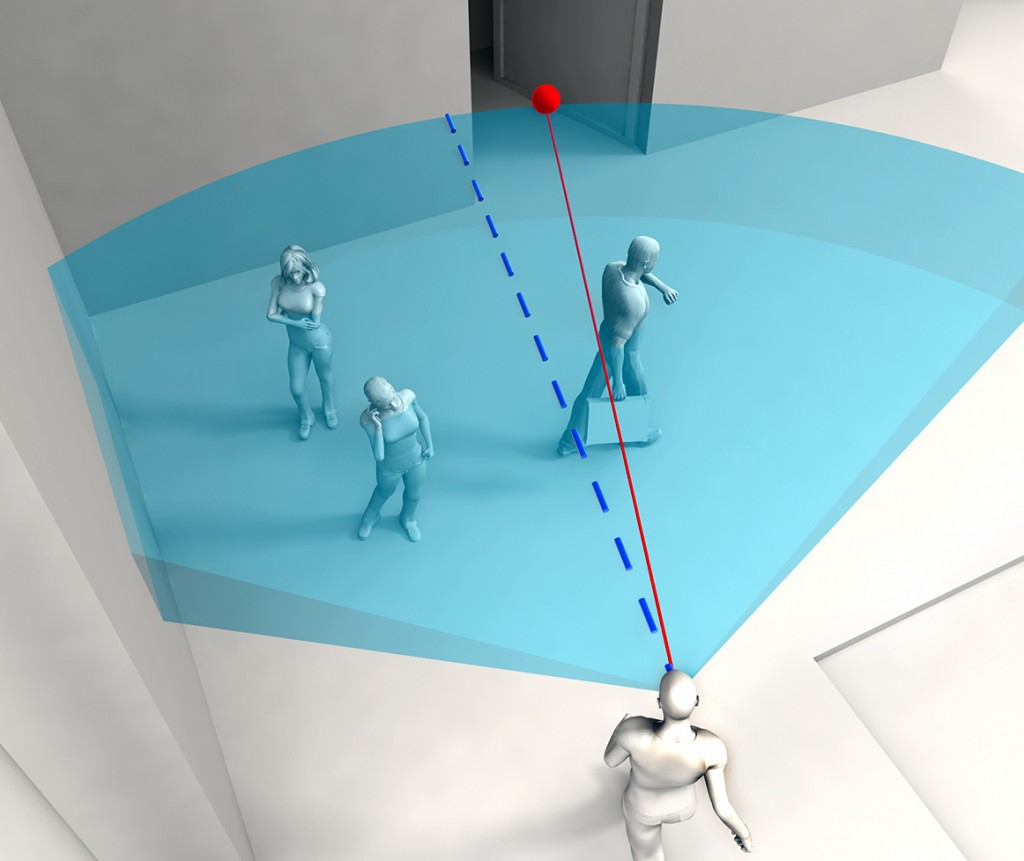
Real crowds in virtual environments
Understanding the collective dynamics of crowd movements during stressful emergency situations is central to reducing the risk of deadly crowd disasters. Yet, their systematic experimental study remains a challenging open problem due to ethical and methodological constraints.